Vyvážený vyhľadávací strom
Vyhľadávací strom
Zovšeobecnenie spojkového zoznamu, kde jeden prvok má viac smerníkov.
- Každý uzol má nula alebo viac podradených uzlov (synov).
- Uzol, ktorý nemá nadradený uzol sa nazýva koreň stromu.
- Uzol, ktorý nemá podradené uzly sa nazýva list.
- Každý uzol je zároveň koreňom podradeného stromu.
Ako to vyzerá v pamäti?
left +------+ right
+--- | 5 | ----+
| +------+ |
v V
left +------+ +------+
+----| 3 | | 10 |
| +------+ +------+
|
V
+------+
| 1 |
+------+Vlastnosti vyhľadávacieho stromu
- Výška stromu: maximálny počet predkov listového uzla. (koľko "poschodí má strom")
- Vyváženosť stromu:: rozdiel medzi ľavou a pravou výškou.
Výška stromu
- Prázdny strom má výšku 0
- maximum z výšky potomkov + 1
Vyváženosť stromu
- Rozdiel vo výške ľavého a pravého syna
- Strom je zle vyvážený, ak je vyváženosť stromu väčšia ako 1 alebo menšia ako -1
Vkladanie prvkov v určitom poradí môže spôsobiť, že na jednej strane môže byť podstatne viac prvkov ako na druhej.
WARNING: Binárny strom sa môže degradovať na spojkový zoznam. Operácia vyhľadávania bude mať lineárnu a nie logaritmickú zložitosť.
Zle vyvážený strom.
Výška 3
left +-----+
+--- | 1 |
| +-----+
v
left +------+
+----| 2 |
| +------+
V
+------+
| 3 |
+------+Vyvážené vyhľadávacie stromy
- počas vkladania alebo vyberania prvku sa vyvažujú
- rotácia stromu: výmena koreňa stromu - vyváženie stromu
Operácie pre vyváženie binárneho stromu
- Ľavá a pravá rotácia
Čo je to rotácia
Operácia ktorá zmení štruktúru stromu, ale nezmení poradie prvkov pri prechádzaní INORDER:
https://en.wikipedia.org/wiki/Tree_rotation
Ľavá rotácia stromu
- Zväčšujeme ľavú výšku a zmenšujeme pravú výšku
- Ak je ľavá výška menšia ako pravá
Ľavá rotácia
ROOT ľavá rotácia PIVOT
/ \ => / \
A PIVOT ROOT C
/ \ / \
B C A BĽavá rotácia
struct node* rotate_left(struct node* parent){
struct node* pivot = parent->right;
assert(pivot != NULL);
parent->right = pivot->left;
pivot->left = parent;
return pivot;
}Pravá rotácia stromu
- Zväčšujeme pravú výšku a zmenšujeme ľavú výšku
- Ak je pravá výška menšia ako ľavá
- zachováme inorder poradie prvkov
Rotácia
ROOT pravá rotácia PIVOT
/ \ => / \
PIVOT C A ROOT
/ \ / \
A B B CPravá rotácia
struct node* rotate_right(struct node* parent){
struct node* pivot = parent->left;
assert(pivot != NULL);
parent->left = pivot->right;
pivot->right = parent;
return pivot;
}Rotácie pre vyváženie stromu
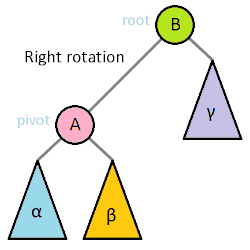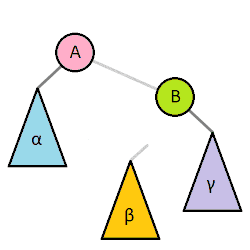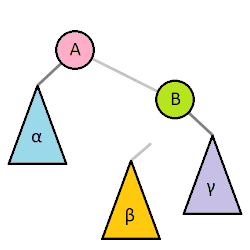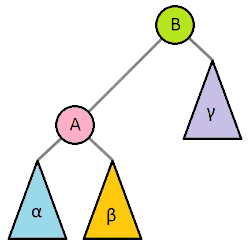
Rotácie pre vyváženie stromu
- Ľavá rotácia zvýši výšku stromu na ľavej strane
- Pravá rotácia zvýši výšku stromu na pravej strane
Vyvážené vyhľadávacie stromy
Pri vkladaní a vyberaní prvkov sa strom vyvažuje pomocou rotácií.
- Avelson-Veltski-Landis tree
- Red-Black tree
- 2-3 tree
- B-tree
AVL strom
Koeficient vyváženia:: rozdiel medzi výškou pravého a ľavého syna.
Každý uzol AVL stromu má koeficient vyváženia -1, 0 alebo 1.
Vkladanie do AVL stromu
- Vložíme uzol.
- Rotujeme všetky uzly, ktoré sa stali nevyvážené.
Mazanie z AVL stromu
- Rotujeme uzol
- Vymažeme uzol
Zhrnutie
- Pomocou vyhľadávacieho stromu vieme pripraviť asociatívne pole.
- Všetky dôležité operácie majú zložitosť
log(n). - Nevyvážený strom sa degraduje na spojkový zoznam.
- Stromy sa vyvažujú pomocou rotácií.